こんにちは、トイトブルクです!
検算のススメ・図形編
本記事では図形を利用した検算の方法をご紹介します。
まだ【計算ミス撲滅】検算のススメ【概数】を読んでいない方はこちらを先にお読みください。
図形が関係する問題では、図形の特徴を利用した検算が使えます。
図形的におかしくないかをチェックしよう
例1:sin, cos, tanのチェック
三角比の単元では次のような問題が良く問われます。
$$ \sin\theta = \frac{3}{5} $$
のとき
$$\cos\theta, \tan\theta$$
の値を求めよ。ただし\( 0° < \theta < 90° \)
解答は以下の通りです。
\( 0° < \theta < 90° \)のとき、\( \cos\theta > 0 \)であるから、
$$ \cos\theta = \sqrt{1-\left(\frac{3}{5}\right)^2} = \sqrt{1-\frac{9}{25}} = \sqrt{\frac{16}{25}} = \frac{4}{5} $$
$$ \tan\theta = \frac{\sin\theta}{\cos\theta} = \frac{3}{5} \div \frac{4}{5} = \frac{3}{4} $$
検算として次のような図を描いてみます。
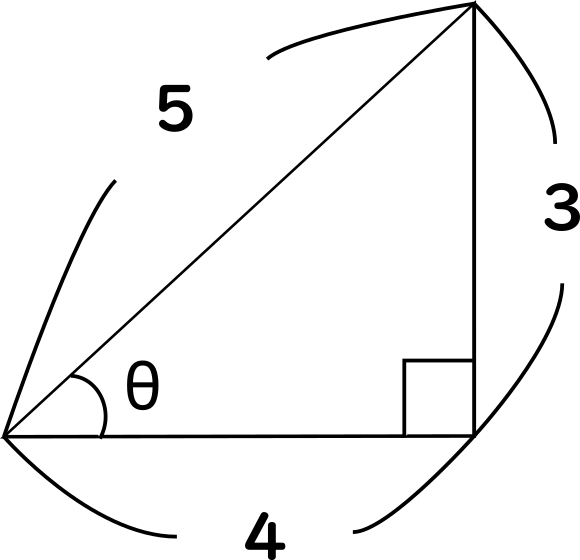
この図を見ると、sin, cos, tanともに値が合っており、直角三角形の条件も満たしていることがわかります。
このように図形的にチェックすると、視覚的に検算ができます。
例2:定積分の値のチェック
今度は定積分の値を図形的にチェックする方法をご紹介します。
下図に示した図形のうち、赤の斜線で囲まれた面積を求めよ。
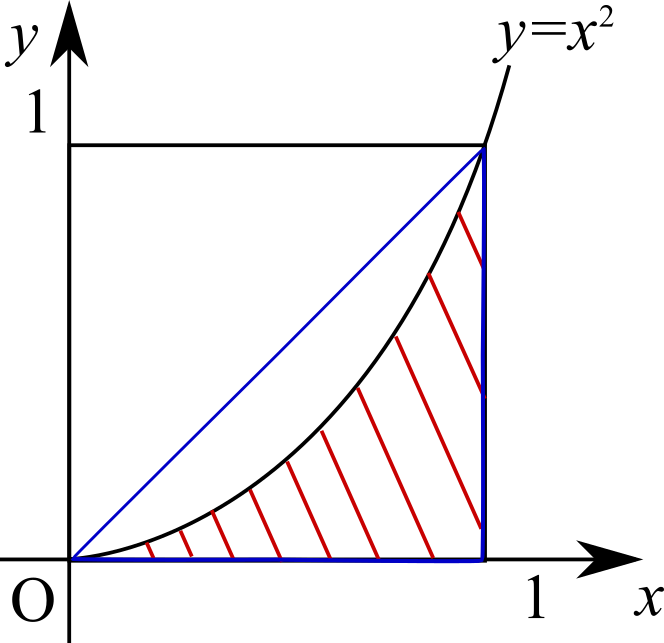
定積分を使って求める。
$$ \int_0^1 x^2 dx = \left[\frac{x^3}{3}\right]_0^1 = \frac{1}{3} $$
この面積について図形的に考えてみます。
まず、面積だから0よりは大きい。
また、青の線で囲まれた三角形の面積\(=\frac{1}{2} \)よりは小さい。
よって
$$ 0 < \int_0^1 x^2 dx < \frac{1}{2} $$
が成り立ちます。
\( \frac{1}{3} \)はこの条件を満たすので、正解の可能性は高いと予測できます。
検算のススメ[図形]:まとめ
- 三角比の問題では、直角三角形を描いて確かめる。
- 定積分で面積を求める問題では、近い形状の図形から面積の当たりをつける。
図形が関係する問題は、上記のように視覚的に検算できます。
さほど時間はかからないので、積極的に検算したいものです。
最後までお読みくださり、ありがとうございました!この記事が少しでもみなさまのお役に立てばうれしく思います。

![アイキャッチ:検算のススメ[図形]](https://toitoburuku-blog.com/wp-content/uploads/2019/05/recommending_checking_by_figure.png)


![アイキャッチ:検算のススメ[概数]](https://toitoburuku-blog.com/wp-content/uploads/2019/05/recommending_checking_by_approximate_number-300x169.png)
![アイキャッチ:検算のススメ[不等式]](https://toitoburuku-blog.com/wp-content/uploads/2019/04/recommending_checking_in_inequality-300x169.png)
![アイキャッチ:検算のススメ[方程式]](https://toitoburuku-blog.com/wp-content/uploads/2019/02/recommending_checking_in_equation-300x169.png)
コメント