こんにちは、トイトブルクです!
皆さんは数学Iで登場する必要条件と十分条件について、整理ができていますか?
本記事では、図解すると必要条件・十分条件の関係が直感的に捉えられるというお話をします。
必要条件・十分条件とは?
必要条件・十分条件という言葉になじみのない方のために、必要条件と十分条件の定義を述べておきます。
$$ P \Rightarrow Q のとき $$
- PはQの十分条件である
- QはPの必要条件である
言葉だけだと、矢印の向きと必要条件・十分条件の関係が直感的にわかりません。丸暗記しようとすると混乱しがちです。
図解して必要条件・十分条件を整理しよう
「必要条件・十分条件」が抽象的な言葉だからわかりにくいのです。
具体的な図を描いて理解しましょう。
次の図をご覧ください。
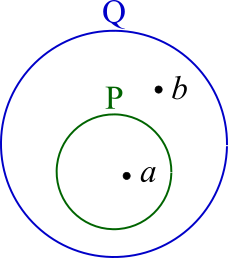
十分条件
上の図で、PはQの中に完全に入っていますが、QはPの中に完全に入っているわけではありません。
点\(a\)と点\(b\)を見ていただければよりわかるかと思います。点\(a\)はPにもQにも入っていますが、点\(b\)はQにしか入っていません。
Pの内側の点は自動的にQの内側に入ります。
言い換えると「PならばQの条件を十分に満たしている」ことになります。これが十分条件です。
必要条件
次にQの内側の点はPの内側に入るとは限りません。しかしPの内側に入るためには最低でもQの内側に入る必要があります。
言い換えると「Qを満たすことはPを満たすのに必要な条件である」ことになります。これが必要条件です。
上の図で\( P \Rightarrow Q \) の矢印の根元は内側、先端は外側と考えましょう。
必要条件・十分条件の問題を図解で解く
では実際の問題をどのように図解で解くか、やってみましょう。
以下の空欄に当てはまる言葉を選択肢a, b, c, dから選べ。
ただし$ x, y$は実数とする。
- (1) \( x = 2 \) は \( x^2 = 4 \)の( )。
- (2) \( x^2 = 4 \) は\( x = 2 \)の( )。
- (3) ひし形であることは長方形であることの( )。
- (4) \( x^2 + y^2 = 0 \)は\( x = y = 0 \)の( )。
- a: 必要条件である
- b: 十分条件である
- c: 必要十分条件である
- d: 必要条件でも十分条件でもない
以下解答です。
(1)と(2)の解答
\( x = 2 \)はこれ以上単純にできません。
次に、\( x^2 = 4 \) より \( x = -2 または x = 2 \)です。
以上を図にするとこうなります。

\( x = 2 \Rightarrow x^2 = 4 \)は成り立ちます。
しかし\( x^2 = 4 \Rightarrow x = 2 \)は成り立ちません(反例:\( x = -2 \))。
以上より
- 「\( x = 2 \) は \( x^2 = 4 \)の十分条件である。」
- 「\( x^2 = 4 \) は\( x = 2 \)の必要条件である。」
と言えます。
【答】 (1) b (2) a
ひし形と長方形の定義を覚えていますか?
- ひし形は「4つの辺の長さが等しい四角形」
- 長方形は「4つの角がすべて等しい四角形」
です。
図にするとこうなります。
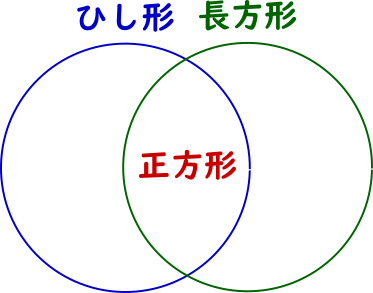
ひし形だからといって長方形とは限らず、長方形だからといってひし形とも限りません。
たまたま両方の条件を満たす(正方形になる)ことはありますが、一方がもう一方の条件を含む関係にはありません。
したがって「ひし形であることは、長方形であることの必要条件でも十分条件でもない」と言えます。
【答】(3) d
\( x^2 + y^2 = 0 \) が成り立つとき、\( x^2 = 0 \) かつ \( y^2 = 0 \) ですから、\( x = 0 \) かつ \( y = 0 \) です。
以上を図にするとこうなります。
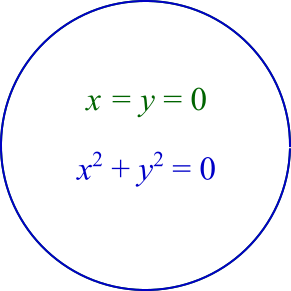
2つの円が一致しています。
- \( x^2 + y^2 = 0 \) ならば \( x = y = 0 \)
- \( x = y = 0 \) ならば \( x^2 + y^2 = 0 \)
です。
こういった関係を「必要十分条件である」といいます。
【答】 (4) c
【図解】必要条件と十分条件:まとめ
- 条件P, Qをできるだけ簡単にする
- 条件P, Qを図に描く
- 狭い円→広い円が十分条件、その逆が必要条件になる
いかがでしたか。
抽象的な「必要」「十分」という言葉を暗記するより、「図解する」ことで必要条件・十分条件の判断がつきやすくなります。
最後までお読みくださり、ありがとうございました!この記事が少しでもみなさまのお役に立てばうれしく思います。



![アイキャッチ:検算のススメ[図形]](https://toitoburuku-blog.com/wp-content/uploads/2019/05/recommending_checking_by_figure-300x169.png)
![アイキャッチ:検算のススメ[概数]](https://toitoburuku-blog.com/wp-content/uploads/2019/05/recommending_checking_by_approximate_number-300x169.png)
![アイキャッチ:検算のススメ[不等式]](https://toitoburuku-blog.com/wp-content/uploads/2019/04/recommending_checking_in_inequality-300x169.png)
![アイキャッチ:検算のススメ[方程式]](https://toitoburuku-blog.com/wp-content/uploads/2019/02/recommending_checking_in_equation-300x169.png)
コメント